Few weeks before Christmas I began looking for a pair of bookshelf speakers. There is a wide spectrum to choose from but I wasn't impressed. After a week of investigations I found that none - within reasonable budget - were capable of going below 50Hz, at least not at -3dB, and there was no mention about their linearity or soundstage. Increasingly disappointed by the offer, I decided to make this one of my next DIY projects.
The start point
in any build is the application of alignment tables on the Thiele/Small parameters of your speaker. In my case - not yet having made a speaker choice - I ran the alignments for a set of mid-woofers within my pre-imposed price range. I ended with a small list out of which I eliminated those yielding high volume boxes or those having rather high cutoff frequencies. Refining the search I ended with the DC160-8 from Dayton, which is a 6.5 inch paper cone speaker with an SPL of 86.1dB @ 2.83V/1m. I chose the 8 Ohm model because this impedance suits most amplifiers.
The alignment getting the best out of this mid-woofer is the SQB4 for a system quality factor Ql = 7. It gives a box of 9.09 liters, a vent resonance frequency of 41.78 Hz and a linear response with a -3dB cut-off at 47.33 Hz.
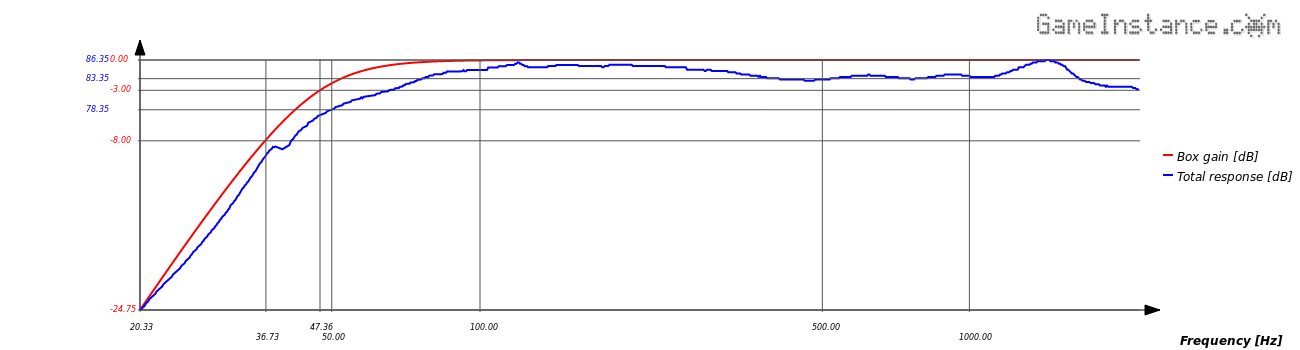 Total frequency response of the system, seen as the SPL of Dayton DC160-8 through the transfer function of the box modeled with SQB4 alignment at Ql=7
Total frequency response of the system, seen as the SPL of Dayton DC160-8 through the transfer function of the box modeled with SQB4 alignment at Ql=7
The frequency response was drawn using the magnitude of the transfer function for a Helmholtz resonator.
where:
As a reminder, Ql is the quality factor of the system and was chosen to be 7 considering a medium sized box with mild dumped interior walls. h=fb/fb is the frequency tuning ratio and is provided by the alignment. α=VAS/VB is the compliance ration and it is given by the alignment as well. VB represents the volume of the vented box.
The Thiele/Small parameters needed to determine the frequency response are fR, QTS and VAS. They represent the free-air resonance frequency of the speaker, its total quality factor and the volume of air having the same compliance as the speaker suspension.
Box sizing
Once the volume of the enclosure is determined, one could use either the golden ratio (1:1.618:0.618) or the acoustical ratio (1:1.2599:0.7937) to size the loudspeaker box. Ideally, it should prevent the formation of any standing waves and needs to have very stiff walls that don't resonate under the excitation of the speaker. The volume of each additional item that needs to be placed inside the box must be accounted for. That includes the bracing, the bass reflex port and the crossover parts.
Adjustments
At the end of the build, some adjustments to the port length must be made to match its resonance frequency to the volume of the result box and the dumping factor of its walls. Otherwise put, if the system has a measured Ql that is different from the initial value 7, port length adjustments must be made. It is generally recommended to start with a slightly longer port and trim it afterwards.
There are applications doing the computations for you and some are free. The purpose of this article is to give you a taste of what's behind those applications. Defining or describing all the terms is beyond the scope of this article. However, reading Vented-box Loudspeaker Systems I and II by Richard Small should give you a good grasp on the subject.