Game Instance

This is a short article on the mathematical formulas modeling the SPL and phase responses of vented loudspeakers. The phase delay and group delay will be defined and discussed towards the end.

Transfer function

in a nutshell, is a 4^th order high-pass filter relying on the Thiele/Small parameters of your speaker. As presented by Herzog and Hilsamer, it is the following:

${\displaystyle G\left(s\right)=\frac{{\left(\frac{s}{\omega }\right)}^4}{1+a_1\left(\frac{s}{\omega }\right)+a_2{\left(\frac{s}{\omega }\right)}^2+a_3{\left(\frac{s}{\omega }\right)}^3+{\left(\frac{s}{\omega }\right)}^4}}$

where: ${\displaystyle a_1=\frac{1}{Q_l\sqrt{h}}+\frac{\sqrt{h}}{Q_{ts}};a_2=\frac{\alpha +1}{h}+h+\frac{1}{Q_l{Q}_{ts}};a_3=\frac{1}{Q_{ts}\sqrt{h}}+\frac{\sqrt{h}}{Q_l};}$

Q_l represents the quality factor of the box. It can be estimated at 7 for a box with average losses or 15 for a better constructed one. The tuning ratio is determined as h=f_b/f_s, where f_b is the resonance frequency of the vent and f_s is the resonance frequency of the speaker. Q_ts is the speaker's total quality factor and it should appear in its datasheet. The α=V_AS/V_B represents the compliance ratio, where V_AS is the volume of air having the same compliance as the speaker and V_B is the effective internal box volume.

Real and Imaginary

Remember that the s is a complex parameter of the form ${\displaystyle s=j\omega }$ where ${\displaystyle \omega =2\pi f}$ and consequently the entire relation G(s) is complex. We thus need the identify the real and imaginary parts of the transfer function.

Replacing all the above, we get ${\displaystyle G\left(\mathrm{j\omega }\right)=\frac{{\hat{\omega }}^4}{(1-a_2{\hat{\omega }}^2+{\hat{\omega }}^4)+j(a_1\hat{\omega }-a_3{\hat{\omega }}^3)}}$ , where ${\displaystyle \hat{\omega }=\frac{\omega }{{\omega }_0}}$ .

The denominator is a complex number, which isn't very helpful, so the relation must be rationalized with the denominator's complex conjugate.

We then get ${\displaystyle G\left(\mathrm{j\omega }\right)=\frac{{\hat{\omega }}^4[(1-a_2{\hat{\omega }}^2+{\hat{\omega }}^4)-j(a_1\hat{\omega }-a_3{\hat{\omega }}^3)]}{{(1-a_2{\hat{\omega }}^2+{\hat{\omega }}^4)}^2+{(a_1\hat{\omega }-a_3{\hat{\omega }}^3)}^2}}$ from which we extract ${\displaystyle Re\left(G\left(\mathrm{j\omega }\right)\right)=\frac{{\hat{\omega }}^4(1-a_2{\hat{\omega }}^2+{\hat{\omega }}^4)}{{(1-a_2{\hat{\omega }}^2+{\hat{\omega }}^4)}^2+{(a_1\hat{\omega }-a_3{\hat{\omega }}^3)}^2}}$, ${\displaystyle Im\left(G\left(\mathrm{j\omega }\right)\right)=\frac{{\hat{\omega }}^4(a_1\hat{\omega }-a_3{\hat{\omega }}^3)}{{(1-a_2{\hat{\omega }}^2+{\hat{\omega }}^4)}^2+{(a_1\hat{\omega }-a_3{\hat{\omega }}^3)}^2}}$.

Frequency response and Phase

can then be determined from the real and imaginary components of the transfer function.

${\displaystyle \left|G\left(s\right)\right|=\sqrt{Re{\left(G\left(s\right)\right)}^2+Im{\left(G\left(s\right)\right)}^2}}$ - the magnitude (frequency response)
${\displaystyle \angle G\left(s\right)={\tan }^{-1}\left[\frac{Im\left(G\left(s\right)\right)}{Re\left(G\left(s\right)\right)}\right]}$ - the phase response, also represented as ${\displaystyle \varphi \left(\omega \right)=arg\left\{G\left(j\omega \right)\right\}}$ .

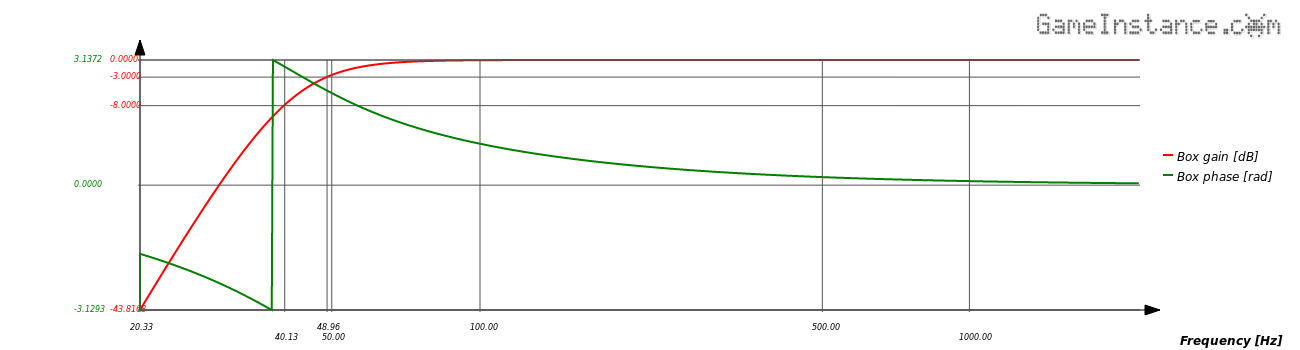Bass-Reflex enclosure modeled with the SQB4, Q_l=15 alignment for a DC160-8 speaker. Frequency response and phase.

Phase and Group delays

are defined using the phase of the transfer function above. They have the meaning of time delay of the phase and time delay of groups of similar frequencies. Both represent a measure of distortion and hence their importance in design evaluation.

${\displaystyle {\tau }_{\varphi }\left(\omega \right)=-\frac{\varphi \left(\omega \right)}{\omega }}$ - the phase delay,
${\displaystyle {\tau }_g\left(\omega \right)=-\frac{d\varphi \left(\omega \right)}{d\omega }}$ - the group delay. 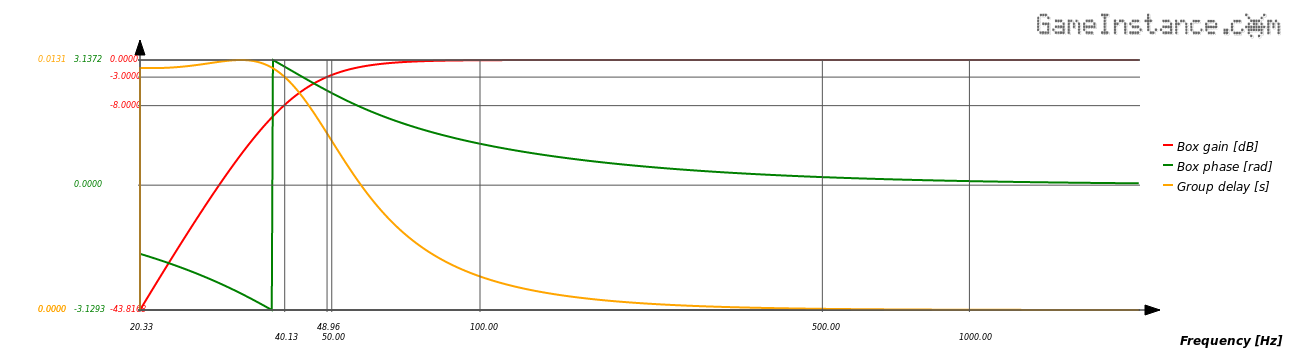Bass-Reflex enclosure modeled with the SQB4, Q_l=15 alignment for a DC160-8 speaker. Frequency response, phase and group delay.

Conclusion

Knowing the transfer function coefficients - the speaker's Thiele/Small parameters and the Q_l - allows the determination of the frequency response for a bass-reflex design. It also gives insights about the rather high group delays that the Bass-Reflex boxes manifest at low frequencies. According to the only known group delay study made by Blauert and Laws, the vented loudspeakers have group delays few times above the human audible thresholds.

The use of low-pass filters for the low frequency driver - passive cross-overs included - accentuates the group delays further more. One solution to this problem is suggested by Herzog and Hilsamer in their article on Low frequency group delay equalization of vented boxes using digital correction filters.